Прямолинейное равномерное движение
Равномерное движение – это движение с постоянной скоростью,
то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение – это движение по прямой линии,
то есть траектория прямолинейного движения – это прямая линия.
Равномерное прямолинейное движение – это движение,
при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде,
то при равномерном движении тело будет перемещаться на одинаковое расстояние за
каждый из этих отрезков времени.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой
точке траектории направлена также, как и перемещение тела. То есть вектор перемещения
совпадает по направлению с вектором скорости. При этом средняя скорость за любой
промежуток времени равна мгновенной скорости:
vcp = v
Скорость равномерного прямолинейного движения – это физическая векторная величина,
равная отношению перемещения тела

за любой промежуток времени к значению этого промежутка t:
 =
=  / t
/ t
Таким образом, скорость равномерного прямолинейного движения показывает,
какое перемещение совершает материальная точка за единицу времени.
Перемещение при равномерном прямолинейном движении определяется формулой:
 =
=  • t
• t
Пройденный путь при прямолинейном движении равен модулю перемещения.
Если положительное направление оси ОХ совпадает с направлением движения,
то проекция скорости на ось ОХ равна величине скорости и положительна:
vx = v, то есть v > 0
Проекция перемещения на ось ОХ равна:
s = vt = x – x0
где x
0 – начальная координата тела,
х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени х = х(t),
принимает вид:
х = x0 + vt
Если положительное направление оси ОХ противоположно направлению движения тела,
то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0),
и тогда уравнение движения принимает вид:
х = x0 - vt
Зависимость скорости, координат и пути от времени
Зависимость проекции скорости тела от времени показана на рис. 1.11.
Так как скорость постоянна (v = const), то графиком скорости является прямая линия,
параллельная оси времени Ot.
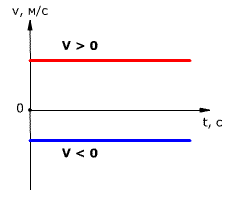
Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.
Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12),
так как величина вектора перемещения равна произведению вектора скорости на время,
за которое было совершено перемещение.
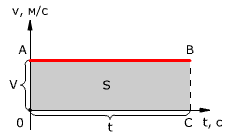
Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
График зависимости перемещения от времени показан на рис. 1.13. Из графика видно,
что проекция скорости равна
v = s1 / t1 = tg α
где α – угол наклона графика к оси времени.
Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость
(больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к
графику зависимости координаты от времени равен скорости:
tg α = v
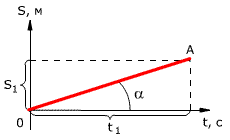
Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.
Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что
tg α1 > tg α2
следовательно, скорость тела 1 выше скорости тела 2 (v
1 > v
2).
tg α3 = v3 < 0
Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть
х = х0
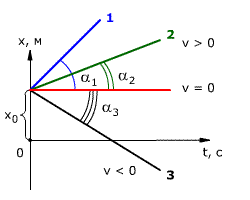
Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.