Равномерное движение по окружности
Равномерное движение по окружности – это простейший пример
криволинейного движения.
Например, по окружности движется конец стрелки часов по циферблату.
Скорость движения тела по окружности носит название линейная скорость.
При равномерном движении тела по окружности модуль скорости тела с течением времени
не изменяется, то есть v = const, а изменяется только направление вектора скорости
 .
Тангенциальное ускорение
в этом случае отсутствует (ar = 0), а изменение вектора скорости по
направлению характеризуется величиной, которая называется центростремительное ускорение
(нормальное ускорение) an или аЦС.
В каждой точке
траектории
вектор центростремительного ускорения направлен к центру окружности по радиусу.
.
Тангенциальное ускорение
в этом случае отсутствует (ar = 0), а изменение вектора скорости по
направлению характеризуется величиной, которая называется центростремительное ускорение
(нормальное ускорение) an или аЦС.
В каждой точке
траектории
вектор центростремительного ускорения направлен к центру окружности по радиусу.
Модуль центростремительного ускорения равен
aЦС=v2 / R
Где v – линейная скорость, R – радиус окружности
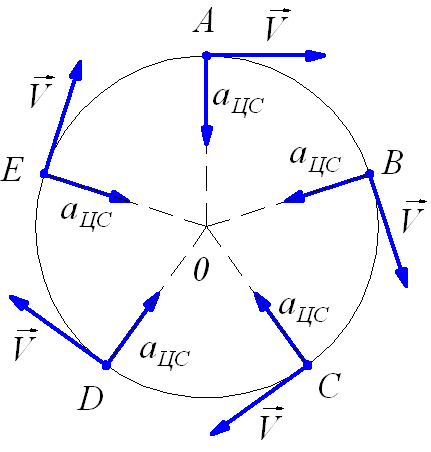
Рис. 1.22. Движение тела по окружности.
Когда описывается движение тела по окружности, используется угол поворота радиуса –
угол φ, на который за время t поворачивается радиус, проведённый из центра
окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота
измеряется в радианах. Радиан равен углу между двумя радиусами окружности, длина дуги
между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то
1 радиан= l / R
Так как длина окружности равна
l = 2πR
то
360о = 2πR / R = 2π рад.
Следовательно
1 рад. = 57,2958о = 57о18’
Угловая скорость равномерного движения тела по окружности – это
величина ω, равная отношению угла поворота радиуса φ к промежутку времени,
в течение которого совершён этот поворот:
ω = φ / t
Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной
скорости определяется отношением длины пройденного пути l к промежутку времени t:
v= l / t
Линейная скорость при равномерном движении по окружности направлена
по касательной в данной точке окружности. При движении точки длина l дуги окружности,
пройденной точкой, связана с углом поворота φ выражением
l = Rφ
где R – радиус окружности.
Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:
v = l / t = Rφ / t = Rω или v = Rω
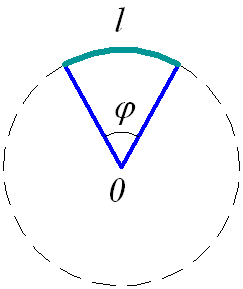
Рис. 1.23. Радиан.
Период обращения – это промежуток времени Т, в течение которого тело (точка)
совершает один оборот по окружности. Частота обращения – это величина,
обратная периоду обращения – число оборотов в единицу времени (в секунду).
Частота обращения обозначается буквой n.
n = 1 / T
За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда
T = 2π / ω
То есть угловая скорость равна
ω = 2π / T = 2πn
Центростремительное ускорение можно выразить через период Т и частоту обращения n:
aЦС = (4π2R) / T2 = 4π2Rn2